Home › Principal

As 11 mais belas equações matemáticas

Por Cesar Grossmann, em 31.01.2013

Equações matemáticas não são apenas úteis – também podem ter uma beleza própria. Muitos cientistas admitem ter preferência por uma ou outra fórmula não só por causa da função, mas pela sua forma, e as verdades simples e poéticas que contém.

Algumas equações, como E=mc² de Einstein, roubam as luzes dos holofotes, mas existem equações menos famosas que têm mais apelo entre cientistas. O LiveScience perguntou a físicos, astrônomos e matemáticos quais suas equações favoritas, e o resultado pode ser conferido a seguir:

11. Equação da Relatividade

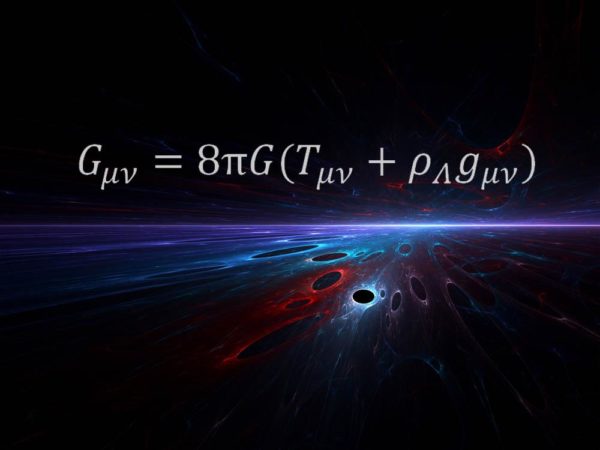
A equação acima foi formulada por Albert Einstein como parte da revolucionária Teoria Geral da Relatividade, em 1915. A teoria mudou a forma como os cientistas entendem a gravidade, ao descrever a força como sendo uma deformação no tecido do espaço-tempo.

O astrofísico Mario Livio, do Space Telescope Science Institute, que escolheu esta equação como sua favorita, aponta que toda a genialidade de Einstein está nela.

“O lado direito da equação descreve o conteúdo de energia do nosso universo, incluindo a energia escura que descreve a aceleração cósmica, e o lado esquerdo descreve a geometria do espaço-tempo. A igualdade reflete o fato que na relatividade geral de Einstein, a massa e energia determinam a geometria, e concomitantemente a curvatura, que é uma manifestação do que chamamos gravidade”, diz Livio.

Kyle Cranmer, físico da Universidade Nova Iorque (EUA), acrescenta que a equação revela a relação entre espaço-tempo, matéria e energia. “Esta equação diz como tudo está relacionado – como a presença do sol deforma o espaço-tempo de forma que a Terra se mova em torno do mesmo em uma órbita, etc. Também diz como o universo evoluiu desde o Big Bang e prediz que devem haver buracos negros nele”.

10. O modelo padrão

Uma das teorias dominantes da física, o modelo padrão descreve a coleção de partículas fundamentais que se acredita fazerem nosso universo.

A teoria pode ser resumida em uma equação chamado modelo padrão lagrangiano (em homenagem a Joseph Louis Lagrange, um matemático e astrônomo francês do século 18), que foi escolhida pelo físico teórico Lance Dixon no Laboratório Acelerador Nacional SLAC na Califórnia (EUA) como sua equação favorita.

“Ela tem descrito com sucesso todas as partículas elementares e forças que temos observados no laboratório até hoje – exceto a gravidade, e isto inclui, é claro, o bóson de Higgs recentemente descoberto, que é o phi na fórmula. Ela é consistente com a mecânica quântica e a relatividade especial”, disse Dixon.

A teoria do modelo padrão ainda não foi unificada com a relatividade geral, e esta é a razão dela não descrever a gravidade.

9. O Cálculo

As equações anteriores descrevem aspectos particulares do universo, mas esta pode ser aplicada a todas as situações. Trata-se do teorema fundamental do cálculo, é o fundamento do método matemático conhecido como cálculo, e une duas ideias: o conceito de integral e o conceito de derivada.

“Em termos simples, ela diz que a mudança geral de uma quantidade contínua, como a distância percorrida, sobre um determinado intervalo, é igual à integral da taxa de mudança daquela quantidade, ou seja, a integral da velocidade”, aponta Melkana Brakalova-Trevithick, chefe do departamento de matemática da Universidade Fordham (EUA), que escolheu esta equação como sua favorita. “O teorema fundamental do cálculo permite que a gente determine a alteração geral sobre um intervalo baseado na taxa de mudança sobre o intervalo inteiro”, diz.

As sementes do cálculo vêm de tempos antigos, mas a maior parte dele foi apresentado no século 17 por Isaac Newton e Gottfried Wilhelm Leibniz (independentemente). Newton usou o cálculo para descrever o movimento dos planetas em torno do sol e Leibniz criou o cálculo para descobrir a área de gráficos de funções (por exemplo, calcular a área delimitada pela linha representada pela função seno e o eixo das abscissas, ou “x”).

8. Teorema de Pitágoras

O velho e conhecido teorema de Pitágoras, que todo estudante aprende, aponta que, para qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa (o lado maior) é igual à soma dos quadrados do comprimento dos outros dois lados.

“O primeiro fato matemático que me maravilhou foi o teorema de Pitágoras”, disse a matemática Daina Taimina, da Universidade Cornell (EUA). “Eu era uma criança e me parecia tão incrível que ele funcionava na geometria e funcionava com números!”.

7. Equação de Euler

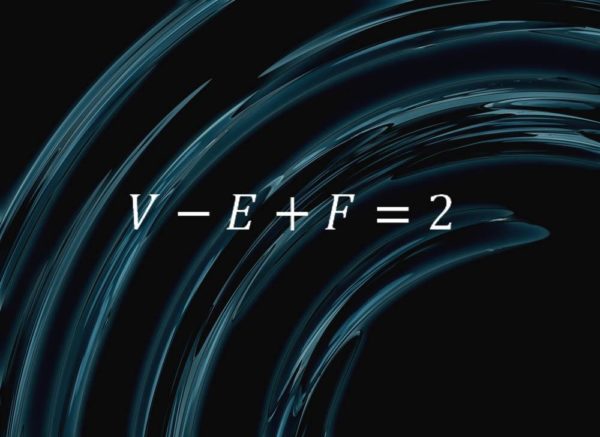
Esta equação simples captura um fato puro sobre a natureza das esferas. “Ela diz que, se você cortar a superfície de uma esfera em faces, arestas e vértices, e chamar de F o número de faces, E o número de arestas, e V o número de vértices, você sempre vai ter V -E + F = 2”, diz Colin Adams, um matemático no Williams College, em Massachusetts (EUA).

“Por exemplo, pegue um tetraedro, consistindo de quatro triângulos, seis arestas e quatro vértices”, explica Adams, “se você soprar com força dentro de um tetraedro com faces flexíveis, você vai curvá-lo em uma esfera, ou seja, de certa forma, uma esfera pode ser cortada em quatro faces, seis arestas, e quatro vértices. E podemos ver que V – E + F = 2. O mesmo vale para uma pirâmide com cinco faces, quatro triangulares e uma quadrada – oito arestas e cinco vértices -, e muitas outras combinações de faces, arestas e vértices”.

6. Relatividade Especial

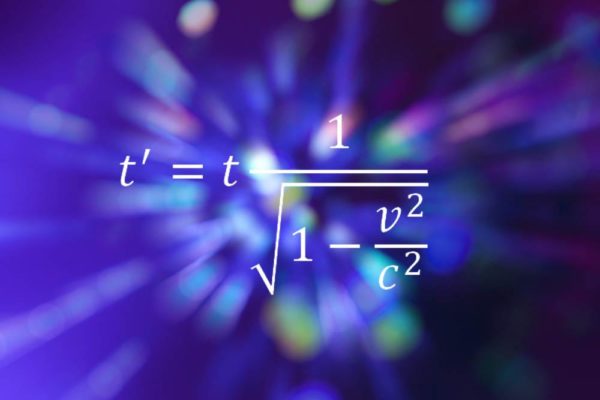
Einstein de novo aparece na nossa lista, desta vez com a fórmula da relatividade especial, que descreve como o tempo e o espaço não são conceitos absolutos, mas relativos, dependendo da velocidade do observador. A equação acima mostra como o tempo dilata, ou contrai, conforme uma pessoa se move mais rápido em qualquer direção.

“O ponto é que ela é realmente muito simples”, diz Bill Murray, um físico de partículas no laboratório CERN, em Genebra. “Não tem nada aí que um estudante não consiga fazer, não tem derivadas complexas, nem álgebra linear. Mas o que ela incorpora é uma forma totalmente nova de ver o mundo, uma atitude em relação à realidade e nosso relacionamento com ela. Subitamente, o cosmos rígido e imutável é varrido para longe e substituído por um mundo pessoal, relacionado com o que você observa. Você se move de uma posição de fora do universo, olhando para baixo, para ser um dos componentes dentro dele. Mas os conceitos e a matemática podem ser compreendidos por qualquer um que queira”, explica.

Murray disse que preferia as equações da relatividade especial às equações mais complicadas da outra teoria de Einstein. “Eu nunca consegui seguir a matemática da relatividade geral”, conta.

5. 1 = 0,9999999….

Esta equação simples, que declara que a quantidade 0,999, seguida por uma sequência infinita de noves, é igual a um, é a equação favorita do matemático Steven Strogatz, da Universidade Cornell.

“Eu adoro como ela é simples – todo mundo entende o que ela diz – e como é provocativa”, diz Strogatz. “Muitas pessoas não acreditam que isto possa ser verdadeiro. É também lindamente equilibrada. O lado esquerdo representa o início da matemática, o lado direito representa os mistérios do infinito”, comenta.

4. Equações Euler-Lagrange e teorema de Noether

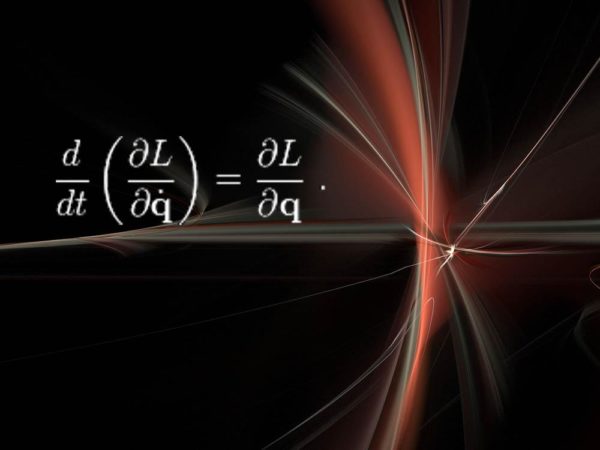
Cranmer, da Universidade Nova Iorque, aponta que estas são equações bastante abstratas, mas extremamente poderosas. “O legal é que esta maneira de pensar sobre física tem sobrevivido a grandes revoluções da área, como a mecânica quântica, a relatividade, etc”.

Nesta equação, o L vem de “lagrangiana”, que é uma medida de energia em um sistema físico, como molas, alavancas ou partículas fundamentais. “Resolver esta equação te diz como o sistema vai evoluir com o tempo”, diz Cranmer.

Uma derivação da equação lagrangiana é chamada de teorema de Noether, em homenagem à matemática alemã do século 20, Emmy Noether. Segundo Cranmer, o teorema é fundamental para a física e mostra a importância da simetria. “Informalmente, o teorema diz que se o seu sistema tem uma simetria, então há uma lei de conservação correspondente. Por exemplo, a ideia que as leis fundamentais da física são todas as mesmas hoje e amanhã (simetria temporal) implica que a energia é conservada. A ideia que as leis da física são as mesmas aqui e no espaço exterior implicam que o momento é conservado. A simetria é talvez o conceito motriz da física fundamental, principalmente devido à contribuição de Noether”, conclui.

3. Equação Callan-Symanzik

“A equação de Callan-Symanzik é uma equação vital dos primeiros princípios a partir de 1970, essencial para descrever como expectativas ingênuas falham em um mundo quântico”, explica o físico teórico Matt Strassler, da Universidade Rutgers (EUA).

É uma equação com numerosas aplicações, entre elas permitir aos físicos estimar a massa e o tamanho do próton e do nêutron, que fazem parte do núcleo dos átomos.

A físcia básica diz que a força gravitacional e a força elétrica entre dois objetos é proporcional ao inverso do quadrado da distância entre eles. Em um nível básico, o mesmo é verdadeiro para a força nuclear forte, que mantém unidos prótons e nêutrons no núcleo atômico, e mantém os quarks juntos para formar prótons e nêutrons. Entretanto, minúsculas flutuações quânticas podem alterar a dependência que a força tem da distância, o que tem consequências dramáticas com a força nuclear forte.

“Ela impede que esta força diminua em grandes distâncias, e faz com que ela prenda quarks e combine-os para formar prótons e nêutrons no nosso mundo”, aponta Strassler. “O que a equação Callan-Symanzik faz é relacionar este efeito dramático e difícil de calcular, importante quando a distância é próxima do tamanho de um próton, para efeitos mais sutis mas fáceis de calcular, que podem ser medidos quando a distância é muito menor que um próton”.

2. Equação da superfície mínima

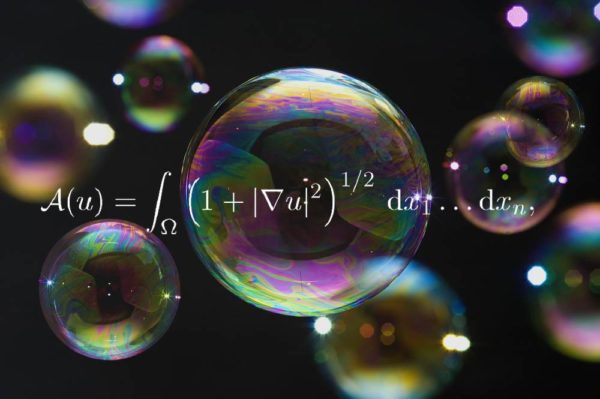
A equação da superfície mínima codifica as belas bolhas de sabão que formam em estruturas de arame quando você as mergulha em água com sabão, aponta o matemático Frank Morgan, do Williams College. “O fato que a equação é ‘não linear’, envolvendo potências e produtos de derivadas, é a dica codificada de forma matemática para o comportamento surpreendente das películas de sabão. Contraste esta equação com equações diferenciais parciais lineares mais familiares, como a equação do calor, a equação da onda, e a equação de Shrödinger para a física quântica”.

1. A reta de Euler

Glen Whitney, fundador do Museu da Matemática em Nova Iorque, escolheu outro teorema geométrico, um que tem a ver com a linha de Euler, que recebeu este nome em homenagem ao matemático e físico suíço do século 18, Leonhard Euler.

“Comece com qualquer triângulo, desenhe o menor círculo que contenha o triângulo e encontre seu centro. Encontre o centro de massa do triângulo – o ponto onde o triângulo, se fosse cortado em uma folha de papel, se equilibraria sobre a ponta de um alfinete. Desenhe as três alturas do triângulo (as linhas que partem de cada canto, perpendiculares ao lado oposto), e encontre o ponto em que elas se encontram. O teorema afirma que todos os três pontos que você encontrou sempre estão sobre uma única linha reta, chamada de ‘reta de Euler‘ do triângulo”, explica Whitney.

Segundo Whitney, o teorema esconde a beleza e o poder da matemática, que geralmente revela padrões surpreendentes em formas familiares e simples.[LiveScience]

Compartilhe:

Curta no Facebook: