Supercomputador revela o nono número de Dedekind: Uma conquista matemática extraordinária
Matemáticos obtiveram recentemente uma descoberta significativa ao encontrar um novo número de Dedekind, com a ajuda de um supercomputador. Esse número recém-descoberto é o nono de sua espécie e é denotado como D(9).
Em forma numérica, D(9) equivale a 286.386.577.668.298.411.128.469.151.667.598.498.812.366, um número impressionante com 42 dígitos. Vale ressaltar que o número de Dedekind anterior, D(8), que foi encontrado em 1991, possuía 23 dígitos.
Entender os números de Dedekind pode ser desafiador, mesmo para não-matemáticos, devido à complexidade dos cálculos envolvidos e aos números enormes utilizados. De fato, havia dúvidas sobre se D(9) seria descoberto.
Lennart Van Hirtum, um cientista da computação da Universidade de Paderborn, na Alemanha, afirmou que o cálculo de D(9) foi um desafio em aberto por 32 anos, gerando incerteza quanto à possibilidade de determinar esse número.
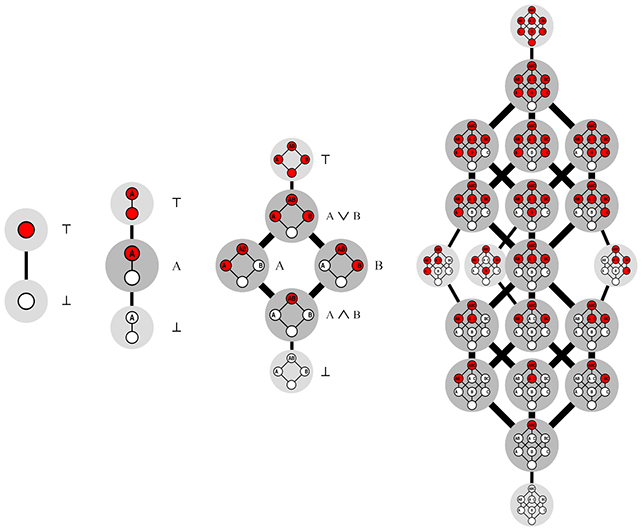
Os números de Dedekind estão relacionados às funções booleanas, que são um tipo de lógica que seleciona saídas com base em entradas compostas apenas por dois estados, como verdadeiro e falso ou 0 e 1.
As funções booleanas monótonas são um tipo específico dessas funções, que possuem uma restrição lógica particular: se uma entrada muda de 0 para 1, a saída pode mudar apenas de 0 para 1 e não de 1 para 0.
Os pesquisadores utilizaram as cores vermelho e branco para representar as funções booleanas, em vez dos números 1 e 0, mas o conceito subjacente permanece o mesmo. Van Hirtum explica que uma função booleana monótona em duas, três ou infinitas dimensões pode ser imaginada como um jogo com um cubo n-dimensional.
O cubo é equilibrado em um dos cantos e os cantos restantes são coloridos de vermelho ou branco. A regra é simples: um canto branco nunca pode ser colocado acima de um vermelho, criando uma interseção vertical vermelha e branca. O objetivo do jogo é contar quantos cortes diferentes existem.
Os primeiros números de Dedekind progridem de maneira direta: D(1) é 2, seguido por 3, 6, 20, 168, 1288, 6532 e assim por diante. A descoberta do D(8) em 1991 foi um marco importante e envolveu a utilização do supercomputador Cray-2, um dos mais poderosos da época. O cálculo levou cerca de 200 horas, com a participação do matemático Doug Wiedemann.
No entanto, o D(9) revelou-se quase duas vezes mais longo que o D(8), apresentando um novo desafio aos pesquisadores. Para enfrentar esse desafio, eles recorreram a um supercomputador especializado chamado Noctua 2.
Entenda o processo de descoberta do novo Dedekind
Esse supercomputador utiliza unidades de processamento chamadas de Field Programmable Gate Arrays (FPGAs), que são capazes de realizar cálculos em paralelo. O Noctua 2, localizado na Universidade de Paderborn, é um dos poucos supercomputadores no mundo que possui a capacidade de lidar com problemas combinatoriais complexos usando FPGAs.
No caso do D(9), a equipe de pesquisadores otimizou o processo ainda mais, utilizando simetrias na fórmula para torná-lo mais eficiente. Eles apresentaram ao Noctua 2 uma soma enorme para calcular, envolvendo aproximadamente 5,5 x 10^18 termos. Essa quantidade é incrivelmente grande e supera a estimativa do número de grãos de areia na Terra (7,5 x 10^18) para efeito de comparação.
Após cinco meses de processamento, o Noctua 2 finalmente encontrou a resposta, revelando o valor de D(9). Essa descoberta é um marco importante na pesquisa dos números de Dedekind e abre caminho para novos estudos e desafios matemáticos.
Embora ainda não tenha sido publicado um artigo de pesquisa detalhando essa descoberta, está prevista uma apresentação sobre o assunto no Workshop Internacional sobre Funções Booleanas e suas Aplicações (BFA), que ocorrerá na Noruega em setembro.
O futuro dos números de Dedekind é ainda incerto, e os matemáticos ainda não fizeram referência a um possível D(10). Considerando o histórico de desafios e complexidades envolvidos, pode ser necessário mais tempo e esforço para desvendar o próximo número dessa sequência fascinante. [ScienceAlert]

