Emaranhamento quântico simplificado

Frank Wilczek explica o conceito de emaranhamento quântico
O conceito de emaranhamento quântico vem acompanhado de uma aura misteriosa que mantém muitas pessoas a uma boa distância. Mas o ganhador do Nobel de Física de 2004, Frank Wilczek, explica o conceito de forma simplificada em sua coluna da revista Quanta Magazine.
“Vou explicar os conceitos de emaranhamento da forma mais simples e clara que puder”, propõe ele.
Emaranhamento é muitas vezes visto como um fenômeno unicamente mecânico quântico, mas não é. Na verdade, fica mais simples de entender se primeiro o considerarmos um evento clássico (ou não quântico), explica Wilczek.
Um emaranhamento acontece em situações em que temos conhecimento parcial sobre o estado de dois sistemas. Por exemplo, nossos sistemas podem ser dois objetos que vamos denominar “c-ons”. O “c” foi escolhido para sugerir que é um evento clássico, mas o físico avisa que, se você preferir, pode escolher qualquer outra palavra que comece com “c”, como chocolate.
Independentes…
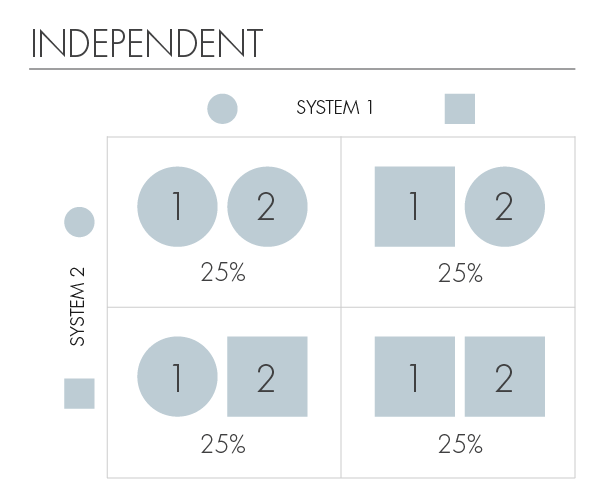
Nossos “c-ons” (ou chocolates) vêm em dois formatos: circular e quadrado, que identificam seus possíveis estados. Então os quatro possíveis estados para esses dois sistemas são: quadrado-quadrado, círculo-quadrado, quadrado-círculo e círculo-círculo. Temos 25% de probabilidade de encontrar cada um desses pares.
Esta é uma situação em que os c-ons são independentes. Se sabemos que o primeiro c-on tem formato de círculo, não temos a mínima ideia do formato do segundo. Ele pode ser um outro círculo, mas também pode ser um quadrado.
… ou emaranhados

Já em uma situação em que eles estão emaranhados, tudo acontece de forma diferente. A informação sobre o primeiro c-on melhora o nosso conhecimento sobre o outro. Temos aqui um caso de emaranhamento extremo: sempre que o primeiro c-on for circular, sabemos que o segundo é circular também. Se o primeiro é um quadrado, o segundo é um quadrado também. Saber o formato de um interfere no formato do outro.
Uma pitadadinha de teoria quântica
A versão quântica do emaranhamento é essencialmente o mesmo fenômeno – ou seja, a falta de independência. Na teoria quântica, estados são descritos como objetos matemáticos chamados Função de Onda. As regras que conectam a função de onda à probabilidade física traz algumas complicações interessantes, mas o conceito central do emaranhamento, que vimos agora há pouco, continua o mesmo.
O emaranhamento entre dois sistemas quânticos acontece naturalmente – por exemplo, no resultado de uma colisão de partículas. Na prática, estados independentes são raras exceções. Quando sistemas interagem, essa interação cria ligação entre eles.
Vamos pensar em moléculas. Elas têm subsistemas chamados elétrons e núcleo. Suas partículas não são independentes, já que conforme o núcleo se move, os elétrons se movem com ele.
Voltando ao nosso exemplo dos c-ons quadrados ou circulares. Há várias formas de criar estados emaranhados. Uma delas é fazer uma medição do sistema que traz uma informação parcial. A partir daí podemos ficar sabendo, por exemplo, que os dois sistemas conspiram para ter o mesmo formato, sem saber exatamente qual o formato deles. Esse conceito será importante mais tarde.
As consequências mais distintivas do emaranhamento quântico são o Paradoxo EPR (Einstein-Podolsky-Rosen) e o Estado de GHZ (Greenberger-Horne-Zeilinger). Elas vêm da interação com outro aspecto da teoria quântica, chamada “complementaridade”.
Complementaridade
É difícil descrever a complementaridade quântica na linguagem comum porque na experiência cotidiana não observamos esse princípio em ação. Mas aperte o cinto e vamos lá!
Até agora imaginamos que nossos c-ons podem ter dois formatos (quadrado e círculo). Mas vamos pensar que eles também podem exibir duas cores: vermelho e azul. Se falarmos de sistemas clássicos, essa propriedade implicaria que nossos c-ons (chocolates clássicos) podem ter quatro estados possíveis: quadrado vermelho, quadrado azul, círculo vermelho, círculo azul.
Já se pensarmos em um q-on (ou uma bela peça de queijo quântico), a situação muda profundamente. O fato que um q-on pode mostrar, em situações diferentes, formatos e cores diferentes, não significa necessariamente que ele possui os dois formatos e cores simultaneamente.

Podemos medir o formato do nossos q-on, mas ao fazermos isso perdemos toda a informação sobre sua cor. Ou podemos medir a cor do nosso q-on, mas perdemos toda a informação sobre o formato. O que não podemos fazer, de acordo com a teoria quântica, é medir o formato e a cor simultaneamente. Essa é a base da complementaridade, conforme Niels Bohr a formulou.
Como consequência, a teoria quântica nos força a ter muito cuidado. Para evitar contradições, devemos levar em consideração que:
1. Uma propriedade que não é medida não existe;
2. A medição é um processo ativo que modifica o sistema sendo medido.
Frank Wilczek descreve duas ilustrações famosas da esquisitice da teoria quântica. As duas foram testadas rigorosamente em experimentos.
Paradoxo Einstein-Podolsky-Rosen

Albert Einstein, Boris Podolsky e Nathan Rosen (EPR) descreveram um efeito que pode acontecer quando dois sistemas quânticos se emaranham. O efeito inclui a complementaridade.
Um par EPR consiste de dois q-on, sendo que cada um pode ter seu formato ou cor medidos (mas não os dois). Levamos em consideração que temos acesso a vários desses pares, todos idênticos, mas que podemos escolher qual medição queremos fazer de seus componentes. Se medirmos o formato de um membro de um par EPR, descobrimos que é igualmente provável que ele seja quadrado ou circular. Se medimos a cor, também descobrimos que é igualmente provável que seja vermelho ou azul.
Os efeitos interessantes, considerados paradoxos por EPR, surgem quando medimos os dois membros do par. Quando os medimos para cor ou para formato, descobrimos que os resultados sempre são iguais. Além disso descobrimos que se um é vermelho e depois medimos a cor do outro, descobriremos que o outro também é vermelho, e assim por diante. Por outro lado, se medimos o formato de um deles e depois a cor do outro, não há correlação. Se o primeiro for um quadrado, o segundo tem igual chance de ser vermelho ou azul.
De acordo com a teoria quântica, vamos obter esses resultados mesmo se existir grande distância entre os dois sistemas, mesmo se as medições forem realizadas quase que simultaneamente. A escolha da medida em um local parece afetar o estado do sistema no outro local. Essa ação à distância assustadora, conforme Einstein a descreveu, parece exigir a transmissão de informação em uma velocidade muito mais rápida que a da luz.
Mas Frank Wilczek questiona: “isso acontece de verdade?”. Até que você conheça o resultado que obteve, você não sabe qual ele é. Fazer a medição não é a mesma coisa que comparar os resultados. E qualquer mensagem revelando o resultado da sua medição será transmitida de forma muito mais lenta que a velocidade da luz. Esse é o paradoxo.
O paradoxo ainda continua: vamos considerar novamente o estado do segundo sistema, levando em conta que o primeiro teve como resultado da medição a cor vermelha. Conforme foi apresentado anteriormente, quando introduzimos complementaridade, se escolhermos medir o formato do q-on, quando ele tem um estado vermelho, vamos ter igual probabilidade de encontrar um quadrado ou círculo como formato. Assim, muito além de introduzir um paradoxo, o EPR é logicamente forçado. Isso é, em essência, simplesmente uma releitura da complementaridade, defende Wilczek.
Além disso, não é paradoxal descobrir que eventos distantes são relacionados. Frank dá um exemplo: se eu colocar um par de cada luva em caixas diferentes e mandá-las pelo correio para lados opostos do planeta, eu não ficaria surpreso ao olhar o conteúdo de uma das caixas e descobrir informações sobre o outro par.
O Estado de GHZ
O trio Daniel Greenberger, Michael Horne e Anton Zeilinger descobriu outro exemplo brilhante de emaranhamento quântico. Ele envolve três q-ons, preparados em um estado especial de emaranhamento (o estado GHZ). Nós distribuímos os três q-ons em três experimentadores distantes. Cada experimentador escolhe, de forma independente e aleatória, se quer medir o formato ou a cor, e registra o resultado. O experimento se repete várias vezes, sempre com os três q-ons começando no mesmo estado GHZ.
Cada experimentador, separadamente, encontra resultados aleatórios. Quando um deles mede o formato de um q-on, tem chances semelhantes de encontrar um quadrado ou um círculo. Quando mede a cor, vermelho ou azul têm a mesma chance de serem encontrados. Nada de novo por aqui.
Mas mais tarde, quando os experimentadores se reúnem para comparar as medições, um pouco de análise revela um resultado incrível. Vamos chamar a forma quadrado e a cor vermelha de “bons”, e as forma circular e a cor azul de “más”. O experimentador percebe que quando dois deles escolhem medir o formato mas o terceiro medir cor, exatamente 0 ou 2 resultados foram “maus” (circulo azul). Mas quando os três decidem medir cor, eles descobrem que exatamente 1 ou 3 medidas são “más”. Isso é o que a mecânica quântica prevê, e é o que é observado.
Então: a quantidade de características “más” é par ou ímpar? As duas possibilidades são obtidas em diferentes formas de medição. Mas somos forçados a rejeitar a questão. Não faz sentido falar sobre a quantidade de características “más” em nosso sistema, independente de como ele é medido. Com certeza isso nos leva a contradições.
O efeito GHZ é, nas palavras do físico Sidney Coleman, “mecânica quântica esfregada na nossa cara”. Isso acaba com um preconceito enraizado na experiência do dia a dia, de que sistemas físicos têm propriedades definitivas, independente de como essas propriedades são medidas. Se fosse assim, o equilíbrio entre o “bom” e o “mal” não seria afetado pela escolha da medição. Uma vez absorvida, a mensagem trazida pelo efeito GHZ é inesquecível.
Pronto, aqui você tem as bases do emaranhamento quântico, envolvendo apenas objetos do dia a dia. Não foi tão simples quanto Frank Wilczek prometeu, mas deu para melhorar um pouquinho a nossa compreensão sobre o assunto, não é? [Quanta Magazine]
