Uma estranha escultura girando em 4D
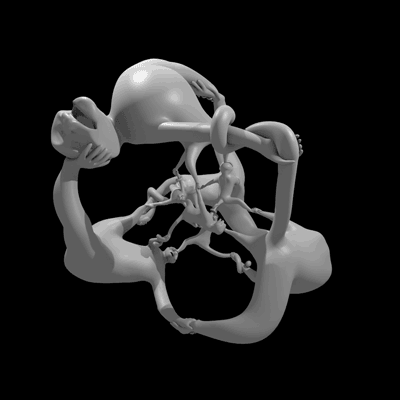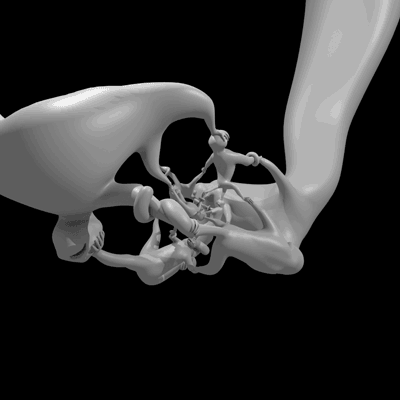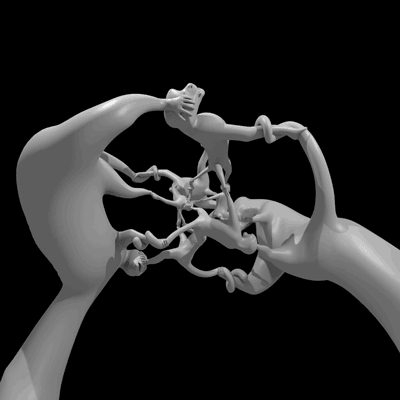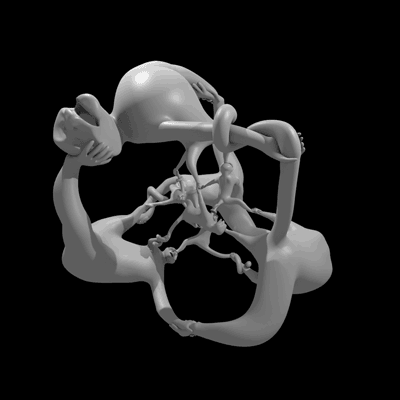
Esta bela figura de seis macacos presos em uma ciranda infinita na quarta dimensão é chamada “More Fun than a Hypercube of Monkeys” e, por incrível que pareça, responde a uma pergunta matemática: será que o grupo quatérnio já apareceu como grupo de simetria de um objeto?
Se isto parece grego para você, o seu consolo é que parece persa arcaico para mim, então vamos destrinchar devagar o que é que o matemático Henry Segerman e o “matemúsico” Vi Hart querem dizer com isso.
Grupos e simetria de grupos
Na matemática, um grupo é um conjunto de elementos que possui associado uma operação que pega dois elementos do grupo e gera um terceiro. Além disso, os grupos precisam ter um elemento de identidade que, quando usado na operação em questão, deixa os outros elementos sem mudanças. Finalmente, eles têm que ter um inverso, ou seja, um elemento que quando participa da operação gera a identidade. Grupos também precisam ter a propriedade da associatividade.
O quatérnio é um grupo com oito elementos, { 1, -1, i, -i, j, -j, k, -k}, e a operação que importa agora é a multiplicação, feita conforme a tabela abaixo:
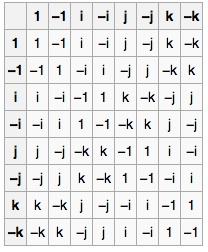
Representação gráfica dos grupos e operações
Bom, como confusão nunca é demais: vamos acrescentar uma forma visual de ver um grupo e suas operações. Podemos pensar que um grupo é um conjunto de transformações visuais. Neste caso, o objeto seria o “1” e a sua reflexão através de uma linha, o “-1”:
No caso da figura da maçã, ainda temos mais uma simetria, a de rotação. Se você girar a maçã por 1/5 de uma volta, que vamos chamar de rotação “a”, a figura não se altera.

A rotação pode ser executada 5 vezes, e sempre gera a identidade. Além disso, a rotação pode ser combinada com a reflexão “-1”. O grupo de transformações visuais pelas quais a maçã pode passar seria “1” (a imagem original), “-1” (a imagem refletida pelo eixo azul), “a” (a rotação de 1/5 de círculo), etc… Representando isto na forma de grupo, teríamos {1, -1, a, -a, a², -a², a³, -a³, a4, -a4} (a² é o resultado de duas rotações de 1/5).
Esta relação entre grupos e simetrias tem sido usada para facilitar o estudo de objetos com simetrias e o estudo de grupos em si, como é o caso do trabalho que criou esta “estátua em 4D”. O objetivo de Hart e Segerman era responder as seguintes questões sobre grupos e simetrias:
- Quais grupos podem ser representados como o grupo das simetrias de objetos físicos do mundo real?
- Quais grupos já foram representados como grupos de simetrias de objetos físicos do mundo real?
- Existem algumas lacunas, grupos pequenos e belos, que deveriam ter uma representação em um objeto simétrico, mas até agora não tiveram?
E é aí que entram os quatérnions. Ou onde eles não entram. O grupo dos quatérnions ainda não apareceu em um grupo de simetria de um objeto físico porque ele não é subgrupo do grupo de simetrias do plano ou do espaço 3D. Em outras palavras, não existe uma combinação de rotações, translações e reflexões em 2 ou 3 dimensões que deixe o espaço intacto e tenha a estrutura do grupo quatérnio.
Nothing Is More Fun than a Hypercube of Monkeys
O grupo de Segerman e Vi Hart resolveram criar um objeto 4D com simetrias descritas pelo grupo quatérnio. Para isto, eles começaram com um objeto 4-Dimensional, o hipercubo. Um hipercubo está para o cubo assim como cubo está para o quadrado. Ou melhor dizendo, se você começar com um ponto e movimentá-lo em uma direção, obtém um segmento de linha. Se você mover a linha em uma direção paralela a ela mesma, vai obter um quadrado. Se mover o quadrado paralelo a si mesmo na terceira dimensão, vai criar um cubo. Se você movimentar o cubo no espaço 4D, paralelo a si mesmo, vai obter o hipercubo ou tesseract.

Não dá para representar um hipercubo, mas dá para fazer a mesma coisa que fazemos ao desenhar uma projeção de um cubo em uma folha: criar uma projeção do hipercubo em um objeto uma dimensão menor, um cubo. Mas, enquanto não temos uma mídia realmente 3D para apresentar a projeção do hipercubo, vocês vão ter que ficar com a imagem animada do hipercubo.

O que os matemáticos fizeram foi colocar um macaco no centro de cada cubo do hipercubo, e obtiveram um objeto 4D que tem suas simetrias descritas pelo quatérnio. O próprio hipercubo não poderia ser usado, já que ele tem um grupo de simetrias maior que o grupo quatérnio, mas ao colocar um macaco – que tem dois braços, duas pernas, uma cauda e uma cabeça – na posição certa no centro de cada cubo do hipercubo, eles acabaram diminuindo o número de simetrias do hipercubo.
A estátua abaixo é a projeção deste objeto 4D no nosso mundo 3D, e foi feita usando uma impressora 3D:
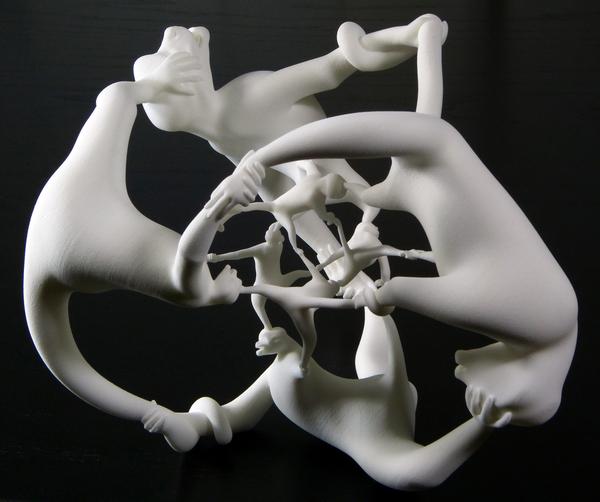
Os pobres macacos tem todos o mesmo tamanho dentro do espaço 4D, mas a projeção deles para o espaço 3D acaba os distorcendo. Se você não tem uma impressora 3D, mas não quer ficar sem esta maravilha matemática, pode comprá-la por US$150 (cerca de R$340). Quem tiver uma hora para perder com estes grupos e macacos e hipercubos, também pode conferir esta fascinante apresentação no Youtube: [Roots of Unity, arXiv, 3ders, The Aperiodical]



1 comentário
Belíssima publicação!
Muito didática, para demonstrar o poder da matemática…