Descoberta Matemática Revolucionária: O Enigma do Número de Dedekind D(9)

Após três décadas de pesquisa incansável, reforçada pelo poder de um supercomputador, matemáticos conseguiram identificar um novo tipo de número primo, conhecido como número de Dedekind. Esse feito representa um avanço significativo na área da matemática.
Essa recente descoberta, denominada D(9), é o nono número de Dedekind e foi calculado como 286 386 577 668 298 411 128 469 151 667 598 498 812 366. Este número de 42 dígitos segue o D(8) de 23 dígitos, encontrado em 1991.
A compreensão do que é um número de Dedekind é algo intrincado, sobretudo para aqueles que não são da área da matemática. O processo envolve cálculos complexos com números extremamente grandes, o que levantou dúvidas sobre a possibilidade de encontrar o D(9).
Lennart Van Hirtum, um cientista da computação da Universidade de Paderborn, na Alemanha, comentou em junho, durante o anúncio desta descoberta, que “Por 32 anos, o cálculo do D(9) foi um desafio em aberto, e era questionável se seria possível calcular esse número”.
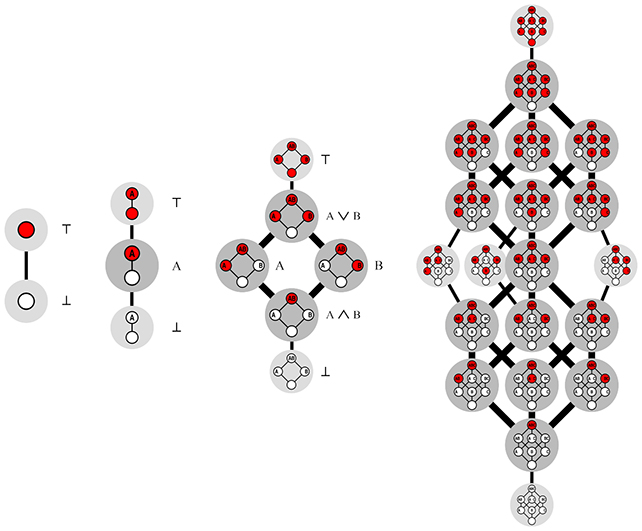
No cerne de um número de Dedekind estão as funções Booleanas, que são um tipo de lógica que determina uma saída a partir de entradas de dois estados, como verdadeiro/falso ou 0/1.
Especificamente, as funções Booleanas monótonas restringem essa lógica de forma que alterar um 0 para 1 na entrada alterará a saída de 0 para 1, mas não o contrário.
A equipe utilizou cores vermelha e branca ao invés de 1s e 0s para explicar esse conceito.
Van Hirtum descreveu: “Imagine uma função Booleana monótona em duas, três e infinitas dimensões como um jogo envolvendo um cubo n-dimensional. Você coloca o cubo em um canto e depois colore cada um dos outros cantos de branco ou vermelho. A única regra é evitar colocar um canto branco acima de um vermelho, criando um limite vertical vermelho-branco. O objetivo é contar o número de interseções diferentes.”
Os primeiros números de Dedekind são mais simples, começando com 2 para D(1), e aumentando para 3, 6, 20, 168 e assim por diante.
Em 1991, o matemático Doug Wiedemann usou um supercomputador Cray-2, um dos mais poderosos da época, por 200 horas para determinar o D(8).
Para o D(9), foi necessário um supercomputador com Arrays de Portas Programáveis em Campo (FPGAs), capaz de realizar cálculos paralelos. Isso levou ao uso do supercomputador Noctua 2 na Universidade de Paderborn.
Christian Plessl, líder do Centro de Computação Paralela de Paderborn (PC2) e responsável pelo Noctua 2, comentou sobre o potencial de usar FPGAs para resolver problemas combinatórios complexos.
Para auxiliar o Noctua 2, otimizações adicionais foram implementadas. Aproveitando as simetrias na fórmula, o processo foi agilizado, fornecendo ao supercomputador uma equação massiva envolvendo 5.510^18 termos (para comparação, estima-se que existam 7.510^18 grãos de areia na Terra).
Após um período de cálculo de cinco meses, o Noctua 2 produziu o resultado, levando à descoberta do D(9). Até o momento, não houve menção à busca pelo D(10) – uma façanha que pode levar mais 32 anos.
Este avanço representa um marco na história da matemática e da computação, mostrando como a colaboração entre estas duas áreas pode levar a descobertas impressionantes. O uso de supercomputadores para resolver problemas matemáticos complexos é um exemplo claro de como a tecnologia pode impulsionar a pesquisa científica. A busca pelo D(9) não foi apenas uma jornada matemática, mas também uma demonstração da evolução e capacidade dos sistemas computacionais.
A descoberta de números de Dedekind como o D(9) ajuda a expandir nosso entendimento sobre estruturas matemáticas complexas e abre caminho para novas investigações em teoria dos números e lógica. Cada novo número de Dedekind encontrado nos oferece uma janela para as profundezas dos números e suas propriedades intrincadas.
A busca pelo D(10), embora ainda não iniciada, promete ser outra jornada empolgante na interseção da matemática com a tecnologia de ponta. À medida que a tecnologia avança, também crescem as possibilidades de novas descobertas matemáticas, talvez até de uma maneira mais rápida do que as três décadas que levou para encontrar o D(9).
Portanto, este evento não é apenas uma celebração para os matemáticos e cientistas da computação, mas também um testemunho do avanço humano no entendimento do universo matemático. A descoberta do D(9) nos lembra que, com persistência e tecnologia avançada, os limites do conhecimento podem ser continuamente expandidos. [Science Alert]
