Qual o tipo de matéria mais efêmera do universo?

Apesar do desligamento do colisor Tevatron do Fermilab (EUA) há dois anos, e a desmontagem posterior do glorioso detector CDF (aparelho de detecção que registra as trajetórias e as energias de elétrons, fótons e luz hádrons), a colaboração dessas máquinas continua a produzir excelentes resultados para a física, graças à enorme quantidade de dados que se acumularam ao longo dos últimos 10 anos.
Por exemplo, a descoberta de uma nova medida interessante de uma propriedade do top quark – partícula encontrada no Fermilab em 1995, a mais pesada partícula elementar que conhecemos. A propriedade medida é o tempo de vida dos quarks.
Devido aos quarks serem excepcionalmente pesados – 173,3 +/- 1 GeV (1 GeV é igual a um bilhão de elétron-volts) -, eles têm uma grande quantidade de energia para transmitir aos seus produtos de decaimento. Isso tem várias consequências. Uma delas é a sua natureza bastante efêmera. Cálculos teóricos nos permitem prever que, para tal objeto, a vida útil depende do inverso da terceira potência da massa, produzindo um curto espaço de existência de quarks – menos de um trilionésimo de trilionésimo de segundo!
Imaginar um intervalo de tempo tão curto é um enorme desafio. A luz não leva nem sequer 10 E -24 segundos para viajar através de um próton. Como imaginar um quark? Digamos que, se você pudesse viajar daqui até o centro da galáxia Andrômeda no primeiro segundo (esquecendo os limites da relatividade especial por um momento), um top quark criado decairia antes de sua jornada bastante rápida passar por um milímetro de espaço.
Se você parar pra pensar sobre isso, é mais incrível perceber que os físicos podem medir um intervalo de tempo tão curto. Eles conseguem fazer isso porque o tempo de vida de uma partícula é inversamente proporcional à sua largura natural. A largura natural de uma ressonância é a incerteza intrínseca de sua massa em repouso. As duas quantidades são conectadas pelo princípio da incerteza de Heisenberg, expressa na relação energia*tempo “AE * Dt> h/2π”, onde h é a constante de Planck.
A relação de incerteza liga o tempo de duração do processo de ressonância (a vida de uma partícula subnuclear), Dt à incerteza na sua energia de repouso, e AE, à massa. O produto deve ser superior a constante de Planck reduzida, de modo que quanto menor Dt, maior deve ser AE. Mas o que tudo isso realmente significa?
Vamos pensar na vibração de uma corda. Ela produz um som, que é audível se a vibração tem uma frequência superior a 40 Hz e inferior a uns mil Hertz. Se imaginarmos ouvir uma nota muito baixa por um curto intervalo de tempo, vamos ter dificuldade em decidir qual a sua altura exata, porque só ouvimos poucas oscilações da onda.
Partículas elementares não são diferentes – na verdade, todos os fenômenos oscilatórios compartilham a fenomenologia básica a este respeito. Assim, um top quark que vive menos de um trilionésimo de trilionésimo de segundo não consegue se “consolidar” em um campo bem definido. A incerteza resultante pode ser observada porque podemos medir a massa dos quarks, o que, em princípio, pode determinar que alguns deles tinham massas ligeiramente acima ou abaixo da média. A propagação de massas é assim ligada ao tempo de vida da partícula.
A colaboração do CDF produziu exatamente esse tipo de medição. É claro, já que estamos falando de uma propagação da ordem de 1,5 GeV, esta é uma medida difícil de executar: o problema é que a massa de qualquer top quark é medida apenas com uma precisão de ordem de magnitude maior – 10, 20 GeV, dependendo das características particulares da deterioração observada. Nossos detectores de partículas são excelentes dispositivos, mas sua resolução de energia não é boa o suficiente para ir abaixo desse nível. Em uma base estatística, no entanto, pode-se detectar se, em uma amostra de quarks, todos tinham a mesma massa de repouso ou eram ligeiramente diferentes, pra estudar em detalhe a distribuição de massas reconstruídas.
A figura abaixo mostra como a distribuição da massa reconstruída dos principais quarks simulados mudaria se tivéssemos assumido uma largura de 1,5 GeV, 5 GeV, ou 10 GeV. A diferença é pequena. No entanto, com grandes amostras de quarks reconstruídos, pode-se ajustar a distribuição observada de diferentes hipóteses, e obter um intervalo de confiança na largura do top quark.

O resultado da montagem da amostra de dados de diferentes hipóteses de largura é mostrada na figura (2). Isto é o que é chamado de “correia de confiança”: para cada valor da largura medida (no eixo horizontal), pode-se determinar um intervalo de confiança (no eixo vertical), que contém o valor verdadeiro da parte superior da largura de uma dada percentagem das vezes, se a experiência foi repetida várias vezes. A medição real é mostrada por uma seta vertical: isso define o intervalo de confiança para a verdadeira largura entre 1,10 e 4,05 GeV.
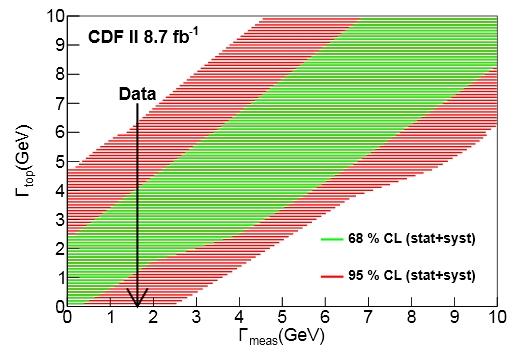
É necessário dizer que esta não é a primeira determinação da largura do top quark; ambos os detectores CDF e DØ produziram tais medidas no passado; DØ, usando alguns pressupostos dependentes do modelo padrão, produziu um resultado mais preciso do que o descrito aqui. Mas o CDF é, contudo, menos afetado por suposições teóricas. [science 2.0]
