Este problema apenas computadores quânticos poderão resolver

Os cientistas da computação Ran Raz (da Universidade de Princeton, nos EUA, e do Instituto Weizmann de Ciência, em Israel) e Avishay Tal (da Universidade de Stanford, nos EUA) encontraram fortes evidências de que os computadores quânticos possuem uma capacidade computacional além de qualquer poder que os computadores clássicos possam alcançar.
A dupla finalmente conseguiu definir um tipo específico de problema computacional que somente os computadores quânticos podem resolver de maneira eficiente.
Pesquisadores têm procurado tal problema desde 1993, quando definiram pela primeira vez uma classe conhecida como “BQP”, que abrange todas as questões que computadores quânticos são capazes de resolver.
Classes de problemas
Uma tarefa básica da ciência da computação teórica é classificar os problemas em classes de complexidade. Uma classe de complexidade contém todos os problemas que podem ser resolvidos usando determinados recursos, como tempo ou memória.
As duas classes de complexidade mais famosas são “P” e “NP”. P são todos os problemas que um computador clássico pode resolver rapidamente, como “Este número é primo?”.
NP são todos os problemas que os computadores clássicos não conseguem resolver rapidamente, mas para os quais podem verificar rapidamente uma resposta se esta for apresentada.
Cientistas da computação acreditam que P e NP são classes distintas, mas provar essa distinção é o problema mais difícil e importante do campo.
BQP
Em 1993, os cientistas da computação Ethan Bernstein e Umesh Vazirani definiram uma nova classe de complexidade chamada de BQP, que significa “tempo polinomial quântico de erro limitado”.
Essa classe contém todos os problemas de decisão – problemas com uma resposta sim ou não – que os computadores quânticos podem resolver de forma eficiente. Na mesma época, a dupla também provou que os computadores quânticos podem resolver todos os problemas que os computadores clássicos conseguem resolver. Ou seja, a classe BQP contém todos os problemas que estão em P.
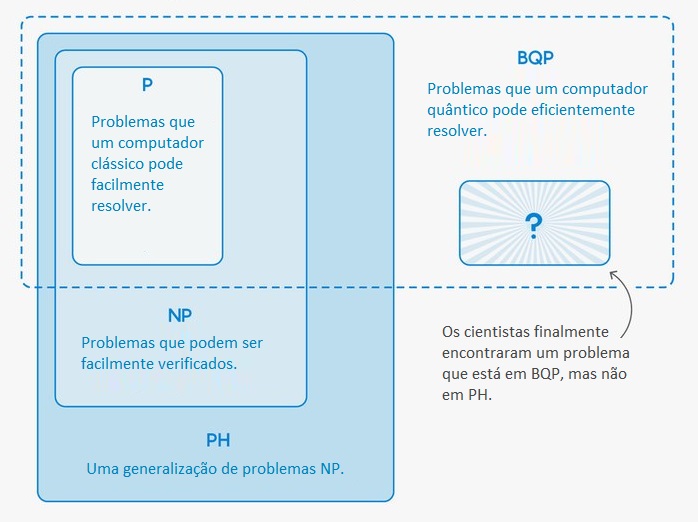
O que eles não puderam determinar é se a BQP contém problemas não encontrados em outra importante classe de problemas conhecida como PH, que significa “hierarquia polinomial”. PH é uma generalização de NP: contém todos os problemas que começam como NP e se tornam mais complexos por conta de instruções qualificadoras (como “para todos…”).
Computadores clássicos hoje não conseguem resolver a maioria dos problemas PH, mas poderiam se P se mostrasse igual a NP. Em outras palavras, comparar a classe BQP à PH é determinar se os computadores quânticos têm uma vantagem sobre os computadores clássicos, vantagem esta que sobreviveria mesmo se os computadores clássicos pudessem (inesperadamente) resolver muitos mais problemas do que podem hoje.
Quântico x clássico
Para fazer o contraste entre as classes BQP e PH, era preciso encontrar um problema que pudesse ser resolvido apenas em BQP – que foi o que Raz e Tal fizeram.
O resultado não significa que computadores quânticos são melhores que os clássicos em qualquer sentido prático.
Por um lado, os pesquisadores já sabiam que os computadores quânticos podiam resolver qualquer problema que os computadores clássicos fossem capazes de lidar. E sequer conseguimos construir uma máquina quântica útil ainda.
Mas a descoberta de Raz e Tal demonstra que os computadores quânticos e clássicos realmente são categorias distintas – mesmo em um mundo onde os computadores clássicos têm sucesso além de todos os sonhos realistas, os computadores quânticos ainda estariam além.
Que problema é esse?
Para identificar um problema exclusivo à BQP, os pesquisadores precisavam de algo que, por definição, um computador clássico não poderia verificar eficientemente a resposta, muito menos encontrá-la.
Scott Aaronson, cientista da computação na Universidade do Texas, nos EUA, sugeriu um bom candidato: imagine que você tenha dois geradores de números aleatórios, cada um produzindo uma sequência de dígitos. A questão para o seu computador é esta: as duas sequências são completamente independentes uma da outra, ou estão relacionadas de alguma maneira oculta, por exemplo, na qual uma sequência é a “transformada de Fourier” da outra?
Aaronson introduziu este problema em 2009, provando que ele pertence à classe BQP. Raz e Tal, agora, provaram que o mesmo problema não está em PH. Para isso, utilizaram uma técnica chamada de “máquina oráculo”.
Oráculo
A melhor maneira de distinguir entre classes de complexidade como BQP e PH é medir o tempo computacional necessário para resolver um problema em cada uma. Mas os cientistas nem sempre têm um entendimento muito sofisticado ou capacidade de medir o tempo real dessa computação.
Assim, para avaliar os tempos de computação impossíveis de medir, eles calculam o número de vezes que um computador precisa consultar um “oráculo” para voltar com uma resposta. A “máquina oráculo” oferece diversas sugestões; você não sabe da onde elas surgem, mas sabe que são confiáveis.
Se o seu problema é descobrir se dois geradores de números aleatórios estão secretamente relacionados, você pode fazer perguntas ao oráculo como “Qual é o sexto número de cada gerador?”, para comparar o poder computacional baseado no número de sugestões que cada tipo de computador usa para resolver o problema. O computador que precisa de mais sugestões é o mais lento.
Raz e Tal mostraram que um computador quântico precisa de muito menos dicas do que um computador clássico para resolver o problema da correlação. Na verdade, precisa de apenas uma dica, enquanto, mesmo com dicas ilimitadas, não há algoritmo em PH que possa resolver o problema.
Esse problema é quântico
O novo trabalho fornece uma garantia de que os computadores quânticos existem em um campo computacional diferente dos computadores clássicos, pelo menos em relação a uma máquina oráculo.
Mesmo em um mundo onde P é igual a NP, a prova de Raz e Tal demonstra que ainda haveria problemas que apenas os computadores quânticos poderiam resolver. [Wired]
