5 surpreendentes fatos matemáticos

A matemática é uma das únicas áreas de conhecimento que podem ser objetivamente descritas como “verdade”, porque seus teoremas são derivados de lógica pura. No entanto, ao mesmo tempo, esses teoremas são extremamente estranho e contra-intuitivos.
Mesmo que você não tenha muita habilidade para trabalhar com matemática (como é o caso deste que vos escreve), certamente se surpreenderá com alguns dos fenômenos listados a seguir:
5. Padrões (não tão) aleatórios
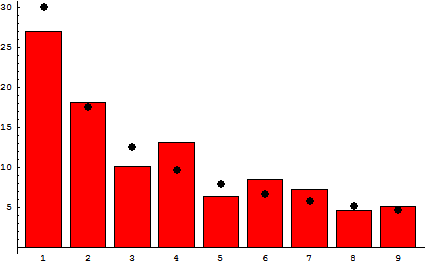
Curiosamente, existem certos padrões até mesmo em listas de dados aparentemente aleatórios (como preços de ações em bolsas de valores e o número de habitantes de cidades): cerca de 30% dos números vão começar com o dígito 1, uma porcentagem menor começará com o dígito 2, uma menor com o 3, e assim por diante, até que apenas um em cada 20 números comece com 9. Quanto maior a lista de números, mais evidente é esse padrão.
4. Espirais de números primos

À primeira vista, números primos (aqueles que só podem ser divididos por 1 e por eles mesmos) são distribuídos sem qualquer ordem entre os números inteiros. Contudo, em 1963, enquanto rabiscava em seu caderno (!), o matemático Stanislaw Ulam percebeu que, se números inteiros forem organizados em uma espiral, números primos sempre caem em linhas diagonais. Esse padrão não é em si tão surpreendente (todos os números primos com exceção do 2 são ímpares, e as espirais se alternam entre pares e ímpares), mas um detalhe gera curiosidade: eles tendem a se agrupar mais em determinadas diagonais do que em outras, independentemente do número que você coloque no começo da espiral – há teorias que procuram explicar o fato, mas nenhuma foi confirmada ainda.
3. Inversão esférica
No ramo matemático da topologia, dois objetos são considerados equivalentes (homomórficos) se puderem ser transformados um no outro apenas esticando e torcendo suas superfícies; se, para fazer isso, for necessário dobrar ou cortar as superfícies, eles são considerados diferentes.
Atentos aos mistérios de sua área de conhecimento, muitos matemáticos se perguntaram: uma esfera e sua versão virada pelo avesso seriam homomórficas? A princípio, pode parecer que não, já que seria necessário furar sua superfície e empurrar a parte interna através do buraco. Contrariando essa ideia inicial, porém, o topologista Bernard Morin descobriu uma forma de virar uma esfera (não material, claro) do avesso respeitando as regras dos objetos “iguais”. Mais surpreendente do que isso é o fato de Morin ser cego, o que dificultou bastante o desenvolvimento da técnica (vista no vídeo acima).
2. Matemática de paredes

Mesmo sendo muitos, há um número finito (matematicamente falando) de padrões geométricos possíveis. Todos os desenhos bidimensionais do artista gráfico Maurits Cornelis Escher (1898 – 1972) se encaixam em um deles (os chamados “grupos de papel de parede”, que são 17 no total).
1. Soneto matemático
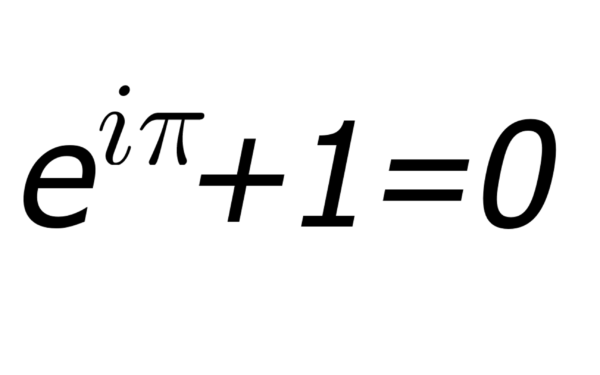
“Como um soneto shakespeareano que captura a própria essência do amor, ou uma pintura que traz a beleza da forma humana e que vai muito além da superfície, a Equação de Euler alcança as profundezas da própria existência”, escreveu o matemático Keith Devlin, em seu artigo “A Mais Bela Equação”, publicado em 2002. De maneira assustadoramente simples, a equação consegue juntar três conceitos matemáticos complexos.
A letra “e” representa um número irracional (com dígitos infinitos) que começa com 2,71828. Descoberto em um estudo sobre o fenômeno de “juros sobre juros”, o “e” aparece em sequências que crescem exponencialmente, como uma população de insetos ou a taxa de decomposição de um elemento radioativo.
Já a letra “i” representa um número imaginário: a raiz quadrada de – 1. Como o próprio nome sugere, esse número desafia as regras da realidade, pois não existe um número que multiplicado por si mesmo resulte em um número negativo – ainda assim, esse estranho número é largamente usado em equações e fórmulas matemáticas complexas.
Por fim, o pi (π) é uma constante que representa o resultado da divisão de uma circunferência por seu diâmetro e também é usado em inúmeras sentenças matemáticas (mais do que os números anteriores).
Na Equação de Euler: “e” elevado a “i x pi” é igual a -1 e, portanto, se somado a 1, é igual a zero. Só me não peçam para explicar como se usa essa equação, pois isso seria abusar de minhas capacidades matemáticas.[LifesLittleMysteries]

17 comentários
A matemática é a ferramenta mais genial já criada pela humanidade, e a capacidade de raciocinar matemáticamente é um verdadeiro presente da natureza.
Sem a matemática, a física seria pura filosofia.
A representação de Euler pode ser facilmente deduzida utilizando-se a série de Taylor para a função f(x) = eˆ(i.x). Assim temos que a expansão deste somatório é igual a: e^(ix) = cos (x) + isen (x). Se ao lugar de x colocarmos um número irracional como PI, teremos: e^(i.PI) = cos (PI) + isen (PI).
Como sabemos pela trigonometria, sen (PI) é igual a 0, portanto a parte Imaginária da equação desaparece da solução e fica apenas a parte Real, cos (PI), que é igual a “1”. Desta forma temos a expressão: e^(i.PI) = 1.
Portanto: e^(i.PI) -1 = 0.
Pequena correção de digitação: cos (PI) = -1. E a solução fica: e^(i.PI) +1 = 0
Sobre os Padrões (não tão) aleatórios, ela é a “Lei de Benford”. Esta freqüência é encontrada em vários dados aleatórios, que podem variar desde o folhear de páginas de um livro, até amostras populacionais. Muitos dados então tendem a esta freqüência, muitos não ficam com o valor exato, mas ficam muito próximos a freqüência desta lei. Agora o que é mais intrigante, é que a sequência de Fibonacci segue muito bem esta Lei, quanto maiores forem os números da sequência de Fibonacci, mais próximo ficaram da Lei de Benford ou números “não tão” aleatórios. Agora observem bem, a sequência de fibonacci é totalmente apoiada na Razão Áurea ou se preferir número de ouro, basta pegar um termo da sequencia de fibonacci e dividir pelo seu antecessor, e o resultado tenderá a 1,618…… que é o número áureo e quanto maiores forem os números da sequência, mais próximo se chega ao resultado.
Já mencionei aqui neste site algumas vezes a Razão Áurea, pois ela está muito mais presente no universo do que podemos imaginar, quem quiser algo interessante, fascinante e instigante, estude a razão áurea, pois sem dúvidas ela esconde ainda muitos conceitos que o ser humano ainda desconhece, pois parece até influenciar dados aleatórios diversos, além de estar muito presente na natureza!
Se aplicarmos a equação de Euler, a espiral de números primos teremos uma espiral infinita de números inteiros.E tambem a espiral de primos se pareçe com a espiral de fibonacci,creio que ambas se superpõem perfeitamente.
Sinto falta de quando a matemática era só 1+1=2
hummm…nem sempre ! 1+1 pode ser 3, pois o todo pode ser maior que a soma de suas partes…
estranho, não ? mas rola ! veja lá “sinergia” e veja se não faz sentido.
calculateprimes.com
Hum ?????
É…por isso nunca escondi que prefiro português! 😉
eu sempr me facinei pela matematica, infelismente não pude estudar.
Não entendi bulhufas nenhuma! O que comprova meus estudos de que odeio matemática!
Fantástico!
Uma coisa que eu gosto muito, e que eu acho que ninguém percebeu (apenas eu e vou contar agora) é que os expoentes de 11 dão na pirâmide de pascal dos coeficientes binomiais… Mas eu não sei demonstrar direito… Tipo 11 ao quadrado é igual a 121 e 1, 2 e 1 são os resultados dos coeficientes binômiais que tem 2 no topo. O mesmo se repete com três já que 11 ao cubo é 1331 e os resultados dos binomiais com 3 no topo é 1,3,3 e 1… O mesmo com 4 já que 11 elevado a quarta é 14641 e os resultados dos binomiais com 4 no topo são 1, 4, 6, 4 e 1. Mas o mesmo não se mistura com os resultados de 5 que apresenta uma falha… Eu nunca entendi, mas sempre escutei que não existem coincidências na matemática :/
quando eu tinha 7 anos meu professor de matemática Carmelo ensinou que na multiplicação feita pelo numero 11 é facil de resolver exemplo 11*11 é so pegar a primeira matriz (o 11 que fica encima ) somar e colocar o resultado no meio dos 2 numeros 1 (fica assim 11*11 P/M 1+1=2 e ai é so colocar o resultado no meio 121 esse é o resultado tchãrã
esse é fácil de provar. lembra da fórmula de (a+b)^n? se sim, é só fazer a=10 e b=1
Comprovando o padrão número 5 com o número de habitantes por cidade no Estado de São Paulo.
Inicia com Cidades
1 179
2 122
3 82
4 84
5 52
6 37
7 38
8 36
9 14