5 fatos matemáticos de quebrar a cabeça
A matemática é uma das áreas do conhecimento que pode objetivamente ser descrita como verdadeira, já que teoremas derivam de pura lógica. Mas, ao mesmo tempo, esses teoremas são geralmente muito estranhos e contra intuitivos.Alguns pensam que matemática é sem graça. Veja os exemplos a seguir: não há nada de entediante!
Em um importante campo da matemática conhecido como topologia, dois objetos são considerados equivalentes, ou homotípicos, se um pode entrar no outro sendo torcido e alongado na superfície; são diferentes, se você tem de cortar ou amassar a superfície para remodelar um dentro do outro.
Uma faixa Moebius — um laço circular com uma única dobra – não são homotípicos com os que não têm a dobra (cilindros), porque você não pode tirar a dobra de uma Moebius sem cortá-la, endireitar um dos cantos e juntar ao outro.
Topologistas refletem: uma esfera é homotípica com sua versão ao avesso? No começo isso parece impossível, já que não é permitido fazer um buraco na esfera e puxar o interior. Mas, de fato, a “eversão da esfera”, como é chamada, é possível. Veja o vídeo acima para saber como é feito.
Incrivelmente, o matemático Bernard Morin, um desenvolvedor chave do complexo método de eversão da esfera, era cego.
Como os números primos são indivisíveis (exceto por um e por eles mesmos), e já que todos os outros podem ser escritos como múltiplos de si, eles são frequentemente lembrados como “átomos” do mundo matemático. Apesar da sua importância, a distribuição dos números primos entre os inteiros ainda é um mistério. Não há um padrão ditando quais números serão primos ou o quão distante eles serão.
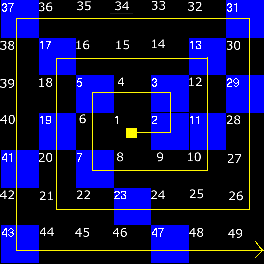
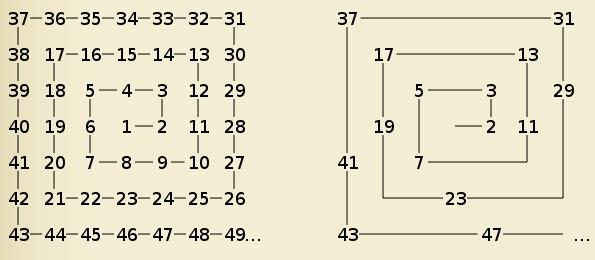
A aparente aleatoriedade dos primos faz do padrão encontrado nas “espirais Ulam” algo muito estranho.
Em 1963, o matemático Stanislaw Ulam notou um estranho padrão enquanto rabiscava em seu caderno em uma apresentação: quando inteiros são escritos em espiral, primos sempre acabam em linhas diagonais. Isso apenas não era tão surpreendente, já que todos os primos exceto o dois são ímpares, e linhas diagonais em espirais inteiras são alternadamente ímpares e pares. Muito mais interessante foi a tendência dos primos de ficar em algumas diagonais mais do que em outras – e isso acontecia não importa se você começasse com o “um” no meio, ou qualquer outro número.
Mesmo quando você forma uma escala muito grande, como na imagem com centenas de números acima, você pode ver linhas diagonais de primos (pontos pretos), com algumas linhas mais fortes que outras. Há algumas tentativas de justificar o porque isso acontecesse, mas nada foi comprovado.

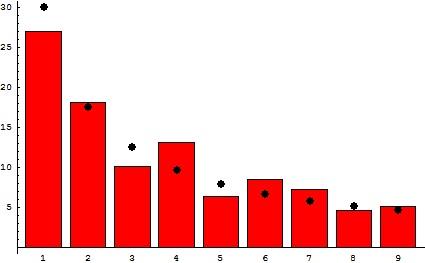
Estranhamente, dados aleatórios não são tão aleatórios. De uma lista de números representando desde preços no mercado de ações até a população de cidades e o tamanho dos prédios, cerca de 30% dos números vão começar com o dígito “um”. Menos com o “dois”, menos ainda com o “três”, e assim por diante, até que apenas um em vinte comece com “nove”. Quanto maior for a amostragem, e maior as grandezas envolvidas, melhor esse padrão aparece.
A fórmula matemática descrevendo a distribuição dos dígitos é chamada de Lei Benford, e sua explicação, descoberta apenas em 1998, tem a ver com logaritmos e leis de poder. Simplificando, ela diz que as mensurações tem mais tendência de começar com o um do que com o nove porque há mais coisas pequenas do que grandes.
A Lei de Benford tem sido usada em casos de fraude pra provar que dados que não se relacionam com a lei devem ser falsos. Até porque, a maioria das pessoas naturalmente pensa que para parecer aleatório, elas devem dar à amostragem um número igual de dígitos.

Apesar de poderem ser decorados com uma variedade infinita de enfeites, matematicamente falando, há apenas um finito número de modelos geométricos distintos. Todas as pinturas de Escher, papéis de parede, design de azulejos e, de fato, todos os arranjos de formas bidimensionais repetidos, podem ser identificados como pertencendo aos chamados “grupos de papéis de parede”. E quantos existem? Exatamente 17.
As classificações desse grupo são baseadas em como os segmentos individuais de um padrão, chamados de células, se encaixam. Para determinar como se encaixam, e em qual grupo, matemáticos testam como eles podem transformar o modelo e ainda acabar com um igual ao original. De acordo com as simetrias que o padrão possuí, ele pode ser categorizado em um dos 17 grupos.
“Como um soneto shakespeariano que captura a essência do amor, ou pinturas que trazem a beleza da forma humana que é muito mais do que a pele, a Equação de Euler atinge os abismos da existência”.
O matemático Keith Devlin escreveu essas palavras sobre a equação acima em 2002, em um artigo chamado “A Mais Bela Equação”. Mas porque a fórmula de Euler é tão fantástica? E o que ela significa?
Inicialmente, a letra “e” representa um número irracional (com dígitos infinitos) que começa com 2,71828… Descoberto no contexto de compostos contínuos, ele dirige a taxa de crescimento exponencial, da população de insetos até a acumulação de interesse e a queda radioativa. Na matemática, o número exibe algumas propriedades surpreendentes, como – usando termos da área – ser igual a soma do inverso de todos os fatores de 0 ao infinito. De fato, a constante “e” permeia a matemática, aparecendo “do nada” em um vasto número de importantes equações.
O “i” representa o chamado “número imaginário”: a raiz quadrada de 1 negativo. Ele é assim chamado porque, na realidade, não há numero que multiplicado por si mesmo produz um negativo (então os negativos não possuem raízes reais). Mas na matemática, há várias situações onde se é forçado a usar a raiz de negativo. A letra “i” então marca os lugares onde isso foi feito.
Pi, a razão de uma circunferência pelo seu diâmetro, é um dos mais amados e conhecidos números na matemática. Como o “e”, ele aparece em uma série de fórmulas matemáticas e físicas.
Colocando tudo junto, a constante “e” elevada ao imaginário “i” multiplicado por Pi é igual a -1. E, como na Equação de Euler, adicionando 1 temos 0. Parece quase impossível que todos esses estranhos números – e até um que não é real – combinariam tão fácil. Mas é um fato comprovado.[Life’sLittleMysteries]

44 comentários
Correção: em dados aleatórios, os dígitos ocorrem na mesma proporção. Quem obedece a Lei de Benford são dados de contagens de coisas que ocorrem naturalmente.
Só uma correção no número 1:
onde está escrito “acumulação de interesse”, leia-se “juros compostos”.
é um quebra-cabeça com poucas soluções exatas
Matemática…ual…
Pra que serve tanta frescura com matemática?
Temos computadores, celulares, e inúmeras coisas grandiosas, que muita gente nem imagina que foram possíveis devido as “frescuras matemáticas”. Visite uma marcenaria, preste atenção a construção de uma casa, a mecânica de um carro e até uma bicicleta, verá exemplos simples de “FRESCURA MATEMÁTICA” que nosso amigo talvez enxergue, mas… acho que foi apenas um comentário infeliz.
A “falha” da probabilidade sobre a utilização dos numeros 1 e 9, 57 anos antes de Frank Bendford, foi observada pelo astrônomo-matemático Simon Newcomb (1835-1909), professor de matemática e astronomia da Johns Hopkins University, e presidente da American Journal of Mathematics.
Olá a todos !
Excelente matéria !
Abraços
me parece que o subtítulo “os leitores mais inteligentes da intenet”. está sendo posto à prova neste post. E 90% deles falharam. 😛
Ser inteligente não obriga a pessoa a entender matemática.
Decerto. A inteligencia é a capacidade de um ser de lidar com as informações que capta no seu derredor. Existe desde os primórdios e , antes, do ser humano dominar a matemática.
Ademais , existem ciências Exatas, Sociais e Humanas.
“Veja os exemplos a seguir: não há nada de entediante!”
Não sei se é pra rir ou chorar. Como não achar entediante? Logo no item “5” não entendi nada.
Acho que o colega que gosta de usar pejorativos deve ser bem fluente em ingles e deveria se candidatar para traduzir alguns textos para o nosso deleite. Afinal, criticas são boas quando são construtivas e voce poderia ter corrigido o erro de tradução sem parecer um mané arrogante…
Acho que o padrão apresentado relativamente aos números primos não passa de uma coincidência (digo eu).
Quem sou eu para colocar em causa a palavra de um matemático. Mas há coisas que não há volta a dar.
Quanto a mim o padrão gerou “linhas” diagonais por causa da figura geométrica sob a qual se inscreveram os números. Será que isso também acontecia se a figura fosse um triângulo ou qualquer outra figura geométrica?
Se as linhas diagonais tivessem realmente a ver com o facto dos números serem primos então essas linhas não seriam interrompidas como acontece.
Tal como em muitos outros exemplos dos anos 50, 60 e 70, algumas das descobertas basearam-se muito em egos exacerbados em que as figuras proeminentes da sociedade gozavam de uma aura de sábios que ninguém ousava contradizer. Talvez também aqui isso tenha acontecido…
Para Grarana Tai. Eu tbm nunca vi uma pessoa tao estupida, aproveitadora e fraca como vc para colocar um comentario tao idiota!! Ve se se toca lol
quando eu era criança fiz isto:
1=9
2=8
3=7
4=6
5
6=4
7=3
8=2
9=1
e que todos numeros na dezena são 1=0 e 0=1
sendo assim
9+9=18 ou seja seguindo a minha regra 1+1=02
6+3=09 ou seja 4+7=11
4+9=13 ou 6+1=07
etc…
porem aprensenta problemas diveria adicionar o 0 em algum lugar ou fazer uma nova regra só não sei aonde ou o que…
porque da isso …5+5=00 e 9.9=72 da isso 1.1=38 mais uma hora eu consigo porque ate agora foi muito bem.
achei legal botei porque acho que alguem acharia interrençante
“interreçante”? interessante ! “Botei”? Entretanto sua observação matemática é muito INTERESSANTE. Explica-se que usamos sistema decimal porque normalmente temos dez dedos mas pode-se representar qualquer numero também no sistema binário.Logo para representar o numero 20 com dedos precisamos duas pessoas.
Fica uma pergunta se tivéssemos apenas dois dedos quantas pessoas precisaríamos para representar o 20? (Sabendo-se que um dedo representa o zero e o outro o numero 1) esse é um exemplo para entender o sistema binário! Acho que seu modelo se relaciona com isso !
As colunas estão em ordem inversa uma da outra,uma sobe outra desce, acho que nesse sentido é que foram colocados sinais de igual entre eles e foram feitas as relações entre eles. Será que entendi ? Acho que sim !
Ela ta tentando arrumar uma formula matemática pra jogar na loteria?
Tenta números satânicos!
uauauauauuhauhauhauhuha
Mas… o que é que isto representa?
Sinceramente não percebi o porquê deste “raciocinio”.
Pode explicar de outra forma?
Tem alguma utilidade?
NUM SEI NEM DIZER
SE A GIRAFA É PRETA COM LISTRAS BRANCAS…
Acho que você quis dizer a zebra, né…
Ha ha ha ha
entao meu amigo voce esta cego
EU NÃO SEI DIZER
O QUE QUER DIZER
O QUE EU VOU DIZER…
Não existe nada mais fascinante do que a Proporção Áurea (Phi = 1,618). Porque está em tudo no Universo. Pitágoras já cantava essa matemágica.
” número irracional (com dígitos infinitos) ”
Parenteses errado. Número racionais também tem dígitos infinitos.
O correto seria dizer que o número irracional, não pode ser escrito como a divisão de dois números inteiros.
Ou então, algo consequente disso, é que o resultado desta divisão (e da divisão de seus restos) nunca formará algo periódico.
Ou seja, enquanto os Racionais formam infinitos digitios periódicos. Os irracionais nunca formam periodicidade.
Sou totalmente burra em matemática 🙁
Não se preocupe! Difícil e complicado é tudo aquilo que não entendemos, mas quando passamos a entender tudo fica fácil, tenho certeza você pode passar a gostar e entender a matemática. Comece a observar exemplos de aplicação da matemática em sua vida diária.Esses exemplos são infinitos, mas é preciso pensar um pouco. Boa Sorte !
A matemática e sua grandiosidade ! Muito boa a matéria !
não entendi bem nem o texto … quanto mais os calculos
A matemática é como nosso universo, grande e misterioso somente para nós, mas tudo que ela representa é lógico, basta agente estender a nossa capacidade de compreende-la.
“(…)Apesar da sua importância, a distribuição dos números primos entre os inteiros ainda é um mistério. Não há um padrão ditando quais números serão primos ou o quão distante eles serão.(…)”
Era mistério até o lançamento do livro Calculate Primes, disponível em calculateprimes.com.
Glauco, você já leu esse livro (Calculate Primes)?
Não, mas vou comprar esse e vários outros em Fevereiro.
Que coisa! O Glauco opina que “era mistério até o lançamento do livro Calculate Prime” sem nunca ter lido o livro! Talvez ele se baseou na suspeita opinião do autor.
Os n°s primos de fato, são e serão a grande incognita matemática de sequencial de todos os tempo. Que existe uma fórmula, eu não tenho dúvida.
Fio
Veja a matéria.
Interessante..
Kis.
Deu pane no meu cérebro aqui!
=/
A demonstração da última afirmação é relativamente fácil usando séries de potências(séries de taylor) e algumas identidades complexas.
Se alguém descobrir algum padrão entre os números primos, fica milionário, a pessoa mais rica do planeta, e entretanto dá cabo de todos os sistemas de segurança e encriptação informáticas, passando a ser a pessoa nº1 para ser assassinada.
Comentário Inteligente !
Ainda bem que existem infinitos números primos! E ainda melhor, a demonstração é a mais fácil de todas!